Another Game of Thrones network analysis - this time with tidygraph and ggraph
A while back, I did an analysis of the family network of major characters from the A Song of Ice and Fire books and the Game of Thrones TV show. In that analysis I found out that House Stark (specifically Ned and Sansa) and House Lannister (especially Tyrion) are the most important family connections in Game of Thrones; they also connect many of the story lines and are central parts of the narrative.
In that old post, I used igraph for plotting and calculating network metrics.
But there are two packages that integrate network analysis much more nicely with the tidyverse: tidygraph and ggraph. These, I am going to show how to use for analyzing yet another network of characters from A Song of Ice and Fire / Game of Thrones (to be correct, this new network here is strictly based on the A Song of Ice and Fire books, NOT on the TV show).
What can network analysis tell us?
Network analysis can e.g. be used to explore relationships in social or professional networks. In such cases, we would typically ask questions like:
- How many connections does each person have?
- Who is the most connected (i.e. influential or “important”) person?
- Are there clusters of tightly connected people?
- Are there a few key players that connect clusters of people?
- etc.
These answers can give us a lot of information about the patterns of how people interact.
So, how do we find out who the most important characters are in this network? We consider a character “important” if he has connections to many other characters. There are a few network properties, that tell us more about this, like node centrality and which characters are key-players in the books.
A word of caution before you read on: BEWARE of SPOILERS for all books!
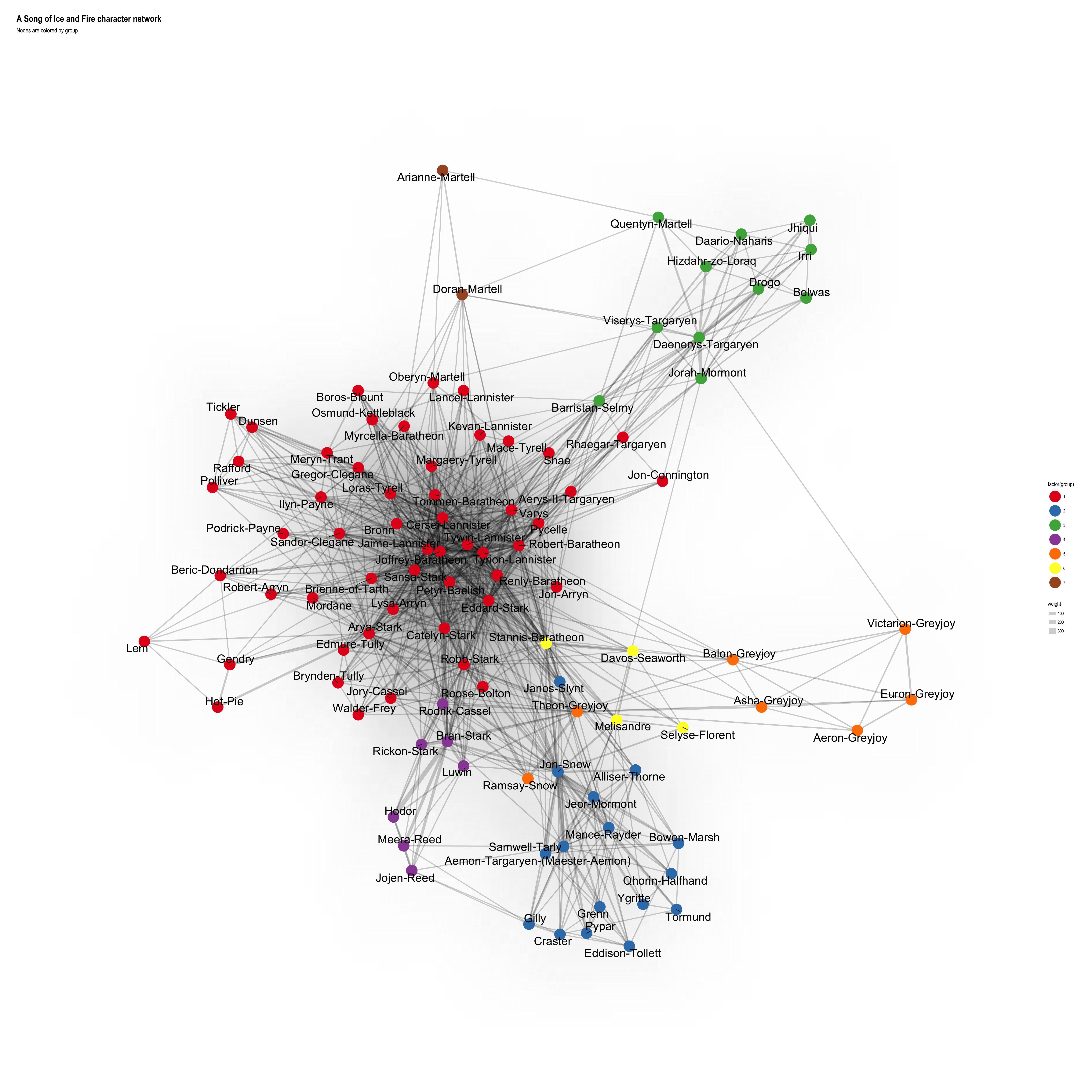
A Song of Ice and Fire character network across all five books; find out how I made it by following the code below…
library(readr) # fast reading of csv files
library(tidyverse) # tidy data analysis
library(tidygraph) # tidy graph analysis
library(ggraph) # for plottingThe Data
I obtained the following data by cloning this Github repository from Andrew Beveridge:
Character Interaction Networks for George R. R. Martin’s “A Song of Ice and Fire” saga These networks were created by connecting two characters whenever their names (or nicknames) appeared within 15 words of one another in one of the books in “A Song of Ice and Fire.” The edge weight corresponds to the number of interactions. You can use this data to explore the dynamics of the Seven Kingdoms using network science techniques. For example, community detection finds coherent plotlines. Centrality measures uncover the multiple ways in which characters play important roles in the saga.
Andrew already did a great job analyzing these character networks and you can read all his conclusions on his site https://networkofthrones.wordpress.com. Here, I don’t aim to replicate his analyses but I want to show how you could do this or similar analyses with tidygraph and ggraph. Thus, I am also not going to use all of his node and edge files.
path <- "/Users/shiringlander/Documents/Github/Data/asoiaf/data/"
files <- list.files(path = path, full.names = TRUE)
files## [1] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-all-edges.csv"
## [2] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-all-nodes.csv"
## [3] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book1-edges.csv"
## [4] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book1-nodes.csv"
## [5] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book2-edges.csv"
## [6] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book2-nodes.csv"
## [7] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book3-edges.csv"
## [8] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book3-nodes.csv"
## [9] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book4-edges.csv"
## [10] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book4-nodes.csv"
## [11] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book45-edges.csv"
## [12] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book45-nodes.csv"
## [13] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book5-edges.csv"
## [14] "/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book5-nodes.csv"Characters across all books
The first data set I am going to use are the character interactions in all five books. I am not using the node files here, because I find the edge names sufficient for this demonstration. If you wanted to have nice name labels, you could use the node files.
cooc_all_edges <- read_csv(files[1])Because there are so many characters in the books, many of them minor, I am subsetting the data to the 100 characters with the most interactions across all books. The edges are undirected, therefore there are no redundant Source-Target combinations; because of this, I gathered Source and Target data before summing up the weights.
main_ch <- cooc_all_edges %>%
select(-Type) %>%
gather(x, name, Source:Target) %>%
group_by(name) %>%
summarise(sum_weight = sum(weight)) %>%
ungroup()
main_ch_l <- main_ch %>%
arrange(desc(sum_weight)) %>%
top_n(100, sum_weight)
main_ch_l## # A tibble: 100 x 2
## name sum_weight
## <chr> <int>
## 1 Tyrion-Lannister 2873
## 2 Jon-Snow 2757
## 3 Cersei-Lannister 2232
## 4 Joffrey-Baratheon 1762
## 5 Eddard-Stark 1649
## 6 Daenerys-Targaryen 1608
## 7 Jaime-Lannister 1569
## 8 Sansa-Stark 1547
## 9 Bran-Stark 1508
## 10 Robert-Baratheon 1488
## # ... with 90 more rowscooc_all_f <- cooc_all_edges %>%
filter(Source %in% main_ch_l$name & Target %in% main_ch_l$name)tidygraph and ggraph
Both tidygraph and ggraph have been developed by Thomas Lin Pedersen:
With tidygraph I set out to make it easier to get your data into a graph and perform common transformations on it, but the aim has expanded since its inception. The goal of tidygraph is to empower the user to formulate complex questions regarding relational data as simple steps, thus enabling them to retrieve insights directly from the data itself. The central idea this all boils down to is this: you don’t have to plot a network to understand it. While I absolutely love the field of network visualisation, it is in many ways overused in data science — especially when it comes to extracting knowledge from a network. Just as you don’t need a plot to tell you which car in a dataset is the fastest, you don’t need a plot to tell you which pair of friends are the closest. What you do need, instead of a plot, is a tool that allow you to formulate your question into a logic sequence of operations. For many people in the world of rectangular data, this tool is increasingly dplyr (and friends), and I do hope that tidygraph can take on the same role in the world of relational data. https://www.data-imaginist.com/2018/tidygraph-1-1-a-tidy-hope/
The first step is to convert our edge table into a tbl_graph object structure. Here, we use the as_tbl_graph() function from tidygraph; it can take many different types of input data, like data.frame, matrix, dendrogram, igraph, etc.
Underneath the hood of tidygraph lies the well-oiled machinery of igraph, ensuring efficient graph manipulation. Rather than keeping the node and edge data in a list and creating igraph objects on the fly when needed, tidygraph subclasses igraph with the tbl_graph class and simply exposes it in a tidy manner. This ensures that all your beloved algorithms that expects igraph objects still works with tbl_graph objects. Further, tidygraph is very careful not to override any of igraphs exports so the two packages can coexist quite happily. https://www.data-imaginist.com/2017/introducing-tidygraph/
A central aspect of tidygraph is that you can directly manipulate node and edge data from this tbl_graph object by activating nodes or edges. When we first create a tbl_graph object, the nodes will be activated. We can then directly calculate node or edge metrics, like centrality, using tidyverse functions.
as_tbl_graph(cooc_all_f, directed = FALSE)## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 1 (active)
## name
## <chr>
## 1 Aemon-Targaryen-(Maester-Aemon)
## 2 Aeron-Greyjoy
## 3 Aerys-II-Targaryen
## 4 Alliser-Thorne
## 5 Arianne-Martell
## 6 Arya-Stark
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 1 4 Undirected 43 7
## 2 1 13 Undirected 44 4
## 3 1 28 Undirected 52 3
## # ... with 795 more rowsWe can change that with the activate() function. We can now, for example, remove multiple edges. When you are using RStudio, start typing ?edge_is_ and wait for the autocomplete function to show you what else is possible (or go to the tidygraph manual).
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(edges) %>%
filter(!edge_is_multiple())## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Edge Data: 798 x 5 (active)
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 1 4 Undirected 43 7
## 2 1 13 Undirected 44 4
## 3 1 28 Undirected 52 3
## 4 1 32 Undirected 53 20
## 5 1 34 Undirected 54 5
## 6 1 41 Undirected 56 5
## # ... with 792 more rows
## #
## # Node Data: 100 x 1
## name
## <chr>
## 1 Aemon-Targaryen-(Maester-Aemon)
## 2 Aeron-Greyjoy
## 3 Aerys-II-Targaryen
## # ... with 97 more rowsNode ranking
Often, especially when visualising networks with certain layouts, the order in which the nodes appear will have a huge influence on the insight you can get out (e.g. matrix plots and arc diagrams). The node_rank_*() family of algorithms have been introduced to provide different ways of sorting nodes so that closely related nodes are positionally close. As there is often not a single correct answer to this endeavor, there’s a lot of different algorithms that may provide different insights into your network. Many of them are based on the seriation package, and the vignette provided therein serves as a nice introduction to the different algorithms. https://www.data-imaginist.com/2018/tidygraph-1-1-a-tidy-hope/
There are many options for node ranking (go to ?node_rank for a full list); let’s try out Minimize hamiltonian path length using a travelling salesperson solver.
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(nodes) %>%
mutate(n_rank_trv = node_rank_traveller()) %>%
arrange(n_rank_trv)## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 2 (active)
## name n_rank_trv
## <chr> <int>
## 1 Gendry 1
## 2 Hot-Pie 2
## 3 Lem 3
## 4 Beric-Dondarrion 4
## 5 Eddard-Stark 5
## 6 Ramsay-Snow 6
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 44 46 Undirected 43 7
## 2 44 45 Undirected 44 4
## 3 44 92 Undirected 52 3
## # ... with 795 more rowsCentrality
Centrality describes the number of edges that are in- or outgoing to/from nodes. High centrality networks have few nodes with many connections, low centrality networks have many nodes with similar numbers of edges. The centrality of a node measures the importance of it in the network.
This version adds 19(!) new ways to define the notion of centrality along with a manual version where you can mix and match different distance measures and summation strategies opening up the world to even more centrality scores. All of this wealth of centrality comes from the netrankr package that provides a framework for defining and calculating centrality scores. If you use centrality measures somewhere in your analysis I cannot recommend the vignettes provided by netrankr enough as they provide a fundamental intuition about the nature of such measures and how they can/should be used. https://www.data-imaginist.com/2018/tidygraph-1-1-a-tidy-hope/
Again, type ?centrality for an overview about all possible centrality measures you can use. Let’s try out centrality_degree().
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(nodes) %>%
mutate(neighbors = centrality_degree()) %>%
arrange(-neighbors)## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 2 (active)
## name neighbors
## <chr> <dbl>
## 1 Tyrion-Lannister 54.
## 2 Cersei-Lannister 49.
## 3 Joffrey-Baratheon 49.
## 4 Robert-Baratheon 47.
## 5 Jaime-Lannister 45.
## 6 Sansa-Stark 44.
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 41 42 Undirected 43 7
## 2 41 60 Undirected 44 4
## 3 41 63 Undirected 52 3
## # ... with 795 more rowsGrouping and clustering
Another common operation is to group nodes based on the graph topology, sometimes referred to as community detection based on its commonality in social network analysis. All clustering algorithms from igraph is available in tidygraph using the group_* prefix. All of these functions return an integer vector with nodes (or edges) sharing the same integer being grouped together. https://www.data-imaginist.com/2017/introducing-tidygraph/
We can use ?group_graph for an overview about all possible ways to cluster and group nodes. Here I am using group_infomap(): Group nodes by minimizing description length using.
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(nodes) %>%
mutate(group = group_infomap()) %>%
arrange(-group)## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 2 (active)
## name group
## <chr> <int>
## 1 Arianne-Martell 7
## 2 Doran-Martell 7
## 3 Davos-Seaworth 6
## 4 Melisandre 6
## 5 Selyse-Florent 6
## 6 Stannis-Baratheon 6
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 32 33 Undirected 43 7
## 2 32 34 Undirected 44 4
## 3 32 36 Undirected 52 3
## # ... with 795 more rowsQuerying node types
We can also query different node types (?node_types gives us a list of options):
These functions all lets the user query whether each node is of a certain type. All of the functions returns a logical vector indicating whether the node is of the type in question. Do note that the types are not mutually exclusive and that nodes can thus be of multiple types.
Here, I am trying out node_is_center() (does the node have the minimal eccentricity in the graph) and node_is_keyplayer() to identify the top 10 key-players in the network. You can read more about the node_is_keyplayer() function in the manual for the influenceR package:
The “Key Player” family of node importance algorithms (Borgatti 2006) involves the selection of a metric of node importance and a combinatorial optimization strategy to choose the set S of vertices of size k that maximize that metric. This function implements KPP-Pos, a metric intended to identify k nodes which optimize resource diffusion through the net … https://cran.r-project.org/web/packages/influenceR/
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(nodes) %>%
mutate(center = node_is_center(),
keyplayer = node_is_keyplayer(k = 10))## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 3 (active)
## name center keyplayer
## <chr> <lgl> <lgl>
## 1 Aemon-Targaryen-(Maester-Aemon) FALSE FALSE
## 2 Aeron-Greyjoy FALSE FALSE
## 3 Aerys-II-Targaryen FALSE FALSE
## 4 Alliser-Thorne FALSE FALSE
## 5 Arianne-Martell FALSE FALSE
## 6 Arya-Stark FALSE FALSE
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 1 4 Undirected 43 7
## 2 1 13 Undirected 44 4
## 3 1 28 Undirected 52 3
## # ... with 795 more rowsNode pairs
Some statistics are a measure between two nodes, such as distance or similarity between nodes. In a tidy context one of the ends must always be the node defined by the row, while the other can be any other node. All of the node pair functions are prefixed with node_* and ends with _from/_to if the measure is not symmetric and _with if it is; e.g. there’s both a node_max_flow_to() and node_max_flow_from() function while only a single node_cocitation_with() function. The other part of the node pair can be specified as an integer vector that will get recycled if needed, or a logical vector which will get recycled and converted to indexes with which(). This means that output from node type functions can be used directly in the calls. https://www.data-imaginist.com/2017/introducing-tidygraph/
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(nodes) %>%
mutate(dist_to_center = node_distance_to(node_is_center()))## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Node Data: 100 x 2 (active)
## name dist_to_center
## <chr> <dbl>
## 1 Aemon-Targaryen-(Maester-Aemon) 1.
## 2 Aeron-Greyjoy 2.
## 3 Aerys-II-Targaryen 1.
## 4 Alliser-Thorne 1.
## 5 Arianne-Martell 2.
## 6 Arya-Stark 1.
## # ... with 94 more rows
## #
## # Edge Data: 798 x 5
## from to Type id weight
## <int> <int> <chr> <int> <int>
## 1 1 4 Undirected 43 7
## 2 1 13 Undirected 44 4
## 3 1 28 Undirected 52 3
## # ... with 795 more rowsEdge betweenness
Similarly to node metrics, we can calculate all kinds of edge metrics. Betweenness, for example, describes the shortest paths between nodes. More about what you can do with edges can be found with ?edge_types and in the tidygraph manual.
as_tbl_graph(cooc_all_f, directed = FALSE) %>%
activate(edges) %>%
mutate(centrality_e = centrality_edge_betweenness())## # A tbl_graph: 100 nodes and 798 edges
## #
## # An undirected simple graph with 1 component
## #
## # Edge Data: 798 x 6 (active)
## from to Type id weight centrality_e
## <int> <int> <chr> <int> <int> <dbl>
## 1 1 4 Undirected 43 7 1.00
## 2 1 13 Undirected 44 4 30.2
## 3 1 28 Undirected 52 3 42.1
## 4 1 32 Undirected 53 20 0.
## 5 1 34 Undirected 54 5 35.2
## 6 1 41 Undirected 56 5 18.9
## # ... with 792 more rows
## #
## # Node Data: 100 x 1
## name
## <chr>
## 1 Aemon-Targaryen-(Maester-Aemon)
## 2 Aeron-Greyjoy
## 3 Aerys-II-Targaryen
## # ... with 97 more rowsThe complete code
Now let’s combine what we’ve done above in true tidyverse fashion:
cooc_all_f_graph <- as_tbl_graph(cooc_all_f, directed = FALSE) %>%
mutate(n_rank_trv = node_rank_traveller(),
neighbors = centrality_degree(),
group = group_infomap(),
center = node_is_center(),
dist_to_center = node_distance_to(node_is_center()),
keyplayer = node_is_keyplayer(k = 10)) %>%
activate(edges) %>%
filter(!edge_is_multiple()) %>%
mutate(centrality_e = centrality_edge_betweenness())We can also convert our active node or edge table back to a tibble:
cooc_all_f_graph %>%
activate(nodes) %>% # %N>%
as.tibble()## # A tibble: 100 x 7
## name n_rank_trv neighbors group center dist_to_center keyplayer
## <chr> <int> <dbl> <int> <lgl> <dbl> <lgl>
## 1 Aemon-Targa… 7 13. 2 FALSE 1. FALSE
## 2 Aeron-Greyj… 85 5. 5 FALSE 2. FALSE
## 3 Aerys-II-Ta… 59 12. 1 FALSE 1. FALSE
## 4 Alliser-Tho… 6 13. 2 FALSE 1. FALSE
## 5 Arianne-Mar… 95 4. 7 FALSE 2. FALSE
## 6 Arya-Stark 34 37. 1 FALSE 1. FALSE
## 7 Asha-Greyjoy 87 7. 5 FALSE 1. FALSE
## 8 Balon-Greyj… 86 11. 5 FALSE 2. FALSE
## 9 Barristan-S… 91 23. 3 FALSE 1. FALSE
## 10 Belwas 42 6. 3 FALSE 2. FALSE
## # ... with 90 more rowscooc_all_f_graph %>%
activate(edges) %>% # %E>%
as.tibble()## # A tibble: 798 x 6
## from to Type id weight centrality_e
## <int> <int> <chr> <int> <int> <dbl>
## 1 1 4 Undirected 43 7 1.00
## 2 1 13 Undirected 44 4 30.2
## 3 1 28 Undirected 52 3 42.1
## 4 1 32 Undirected 53 20 0.
## 5 1 34 Undirected 54 5 35.2
## 6 1 41 Undirected 56 5 18.9
## 7 1 42 Undirected 57 25 0.
## 8 1 48 Undirected 58 110 0.
## 9 1 58 Undirected 60 5 24.5
## 10 1 71 Undirected 62 5 17.0
## # ... with 788 more rowsPlotting with ggraph
For plotting our graph object, we can make good use of the ggraph package:
ggraph is an extension of ggplot2 aimed at supporting relational data structures such as networks, graphs, and trees. While it builds upon the foundation of ggplot2 and its API it comes with its own self-contained set of geoms, facets, etc., as well as adding the concept of layouts to the grammar. https://github.com/thomasp85/ggraph
First, I am going to define a layout. There are lots of options for layouts, here I am using a Fruchterman-Reingold algorithm.
layout <- create_layout(cooc_all_f_graph,
layout = "fr")The rest works like any ggplot2 function call, just that we use special geoms for our network, like geom_edge_density() to draw a shadow where the edge density is higher, geom_edge_link() to connect edges with a straight line, geom_node_point() to draw node points and geom_node_text() to draw the labels. More options can be found here.
Here are three options of plotting the network with the metrics we just calculated:
ggraph(layout) +
geom_edge_density(aes(fill = weight)) +
geom_edge_link(aes(width = weight), alpha = 0.2) +
geom_node_point(aes(color = factor(group)), size = 10) +
geom_node_text(aes(label = name), size = 8, repel = TRUE) +
scale_color_brewer(palette = "Set1") +
theme_graph() +
labs(title = "A Song of Ice and Fire character network",
subtitle = "Nodes are colored by group")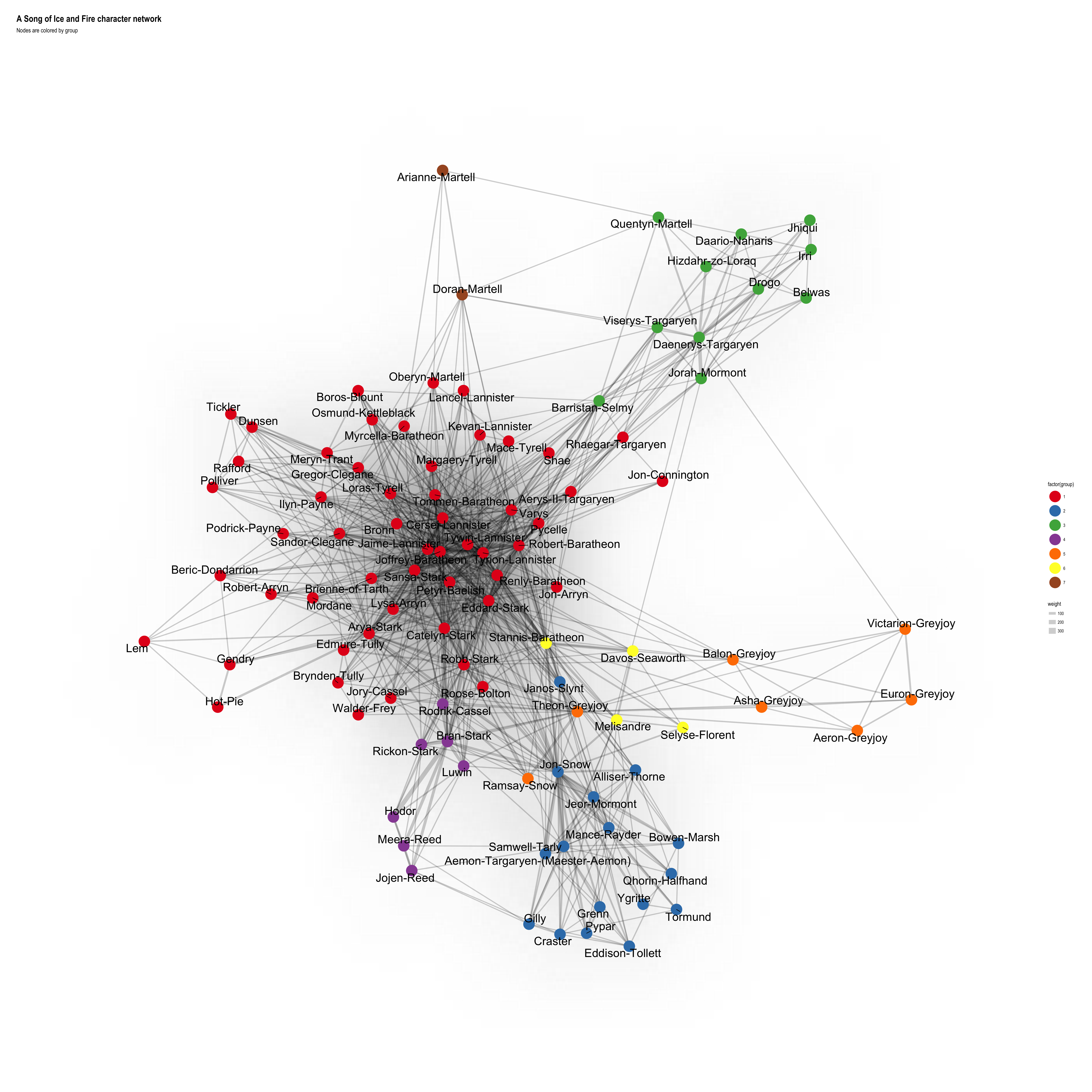
Interestingly, many of the groups reflect the narrative perfectly: the men from the Night’s Watch are grouped together with the Wildlings, Stannis, Davos, Selyse and Melisandre form another group, the Greyjoys, Bran’s group in Winterfell before they left for the North, Dany and her squad and the Martells (except for Quentyn, who “belongs” to Dany - just like in the books ;-)). The big group around the remaining characters is the only one that’s not split up very well.
For the next graphs, I want specific colors form the RColorBrewer palette “Set1”:
cols <- RColorBrewer::brewer.pal(3, "Set1")ggraph(layout) +
geom_edge_density(aes(fill = weight)) +
geom_edge_link(aes(width = weight), alpha = 0.2) +
geom_node_point(aes(color = factor(center), size = dist_to_center)) +
geom_node_text(aes(label = name), size = 8, repel = TRUE) +
scale_colour_manual(values = c(cols[2], cols[1])) +
theme_graph() +
labs(title = "A Song of Ice and Fire character network",
subtitle = "Nodes are colored by centeredness")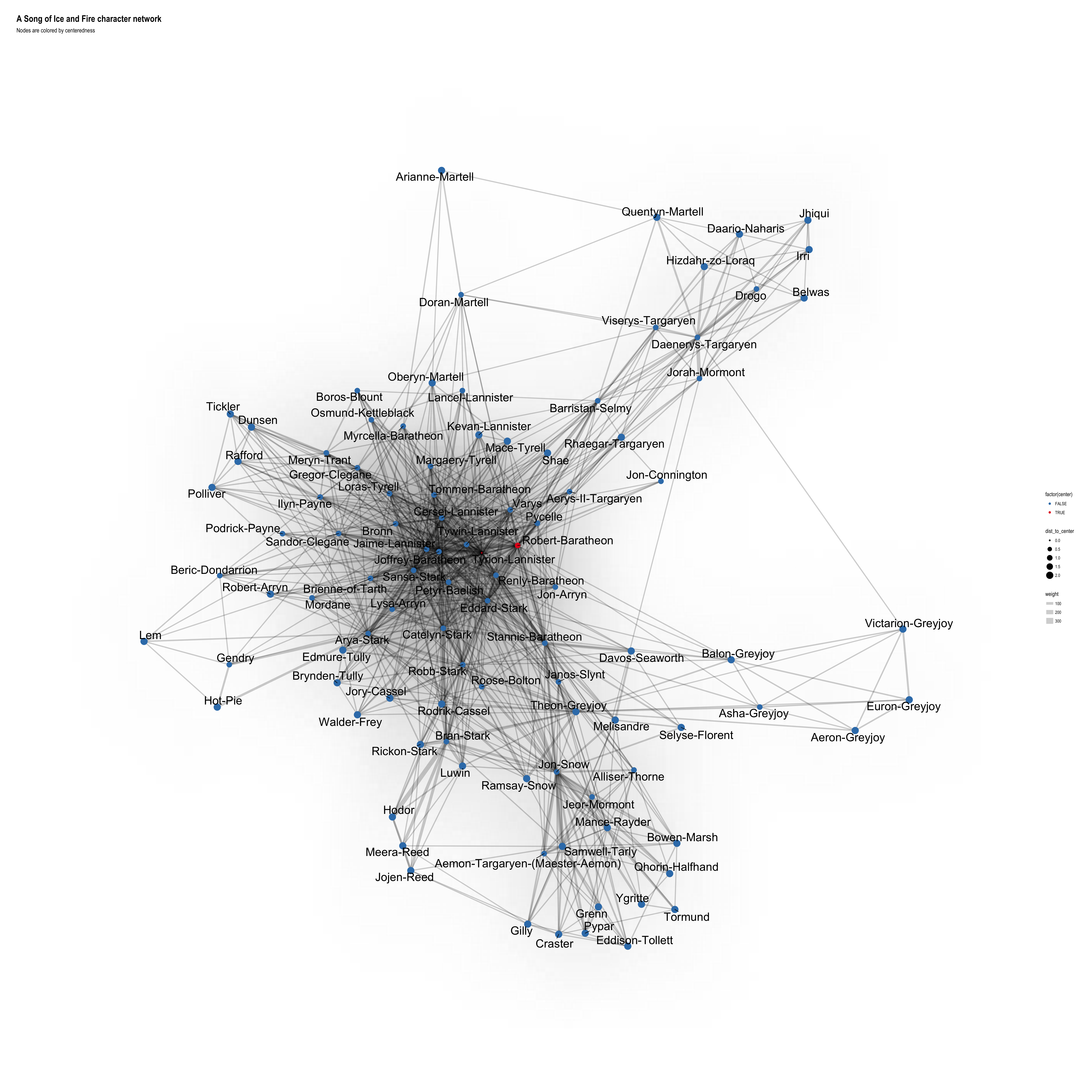
In the next graph I plotted the center-most characters in red and the distance to center as node size. The two center characters across all books are Robert Baratheon and Tyrion Lannister. I had not expected Robert, since he dies pretty much right away but I guess he and his rebellion following Lyanna’s “abduction” is the main trigger for most of what happens in the books, so why not… And that Tyrion is the best character (and George RR Martin’s favorite) is a given, anyways! ;-)
Characters devided by books
The second data set I am going to use is a comparison of character interactions in the five books.
A little node on the side: My original plan was to loop over the separate edge files for each book, concatenate them together with the information from which book they are and then plot them via faceting. This turned out to be a bad solution because I wanted to show the different key-players in each of the five books. So, instead of using one joined graph, I created separate graphs for every book and used the bind_graphs() and facet_nodes() functions to plot them together.
for (i in 1:5) {
cooc <- read_csv(paste0("/Users/shiringlander/Documents/Github/Data/asoiaf/data//asoiaf-book", i, "-edges.csv")) %>%
mutate(book = paste0("book_", i)) %>%
filter(Source %in% main_ch_l$name & Target %in% main_ch_l$name)
assign(paste0("coocs_book_", i), cooc)
}The concepts are the same as above, here I want to know the key-players in each book:
cooc_books_1_graph <- as_tbl_graph(coocs_book_1, directed = FALSE) %>%
mutate(book = "Book 1: A Game of Thrones",
keyplayer = node_is_keyplayer(k = 10))
cooc_books_2_graph <- as_tbl_graph(coocs_book_2, directed = FALSE) %>%
mutate(book = "Book 2: A Clash of Kings",
keyplayer = node_is_keyplayer(k = 10))
cooc_books_3_graph <- as_tbl_graph(coocs_book_3, directed = FALSE) %>%
mutate(book = "Book 3: A Storm of Swords",
keyplayer = node_is_keyplayer(k = 10))
cooc_books_4_graph <- as_tbl_graph(coocs_book_4, directed = FALSE) %>%
mutate(book = "Book 4: A Feast for Crows",
keyplayer = node_is_keyplayer(k = 10))
cooc_books_5_graph <- as_tbl_graph(coocs_book_5, directed = FALSE) %>%
mutate(book = "Book 5: A Dance with Dragons",
keyplayer = node_is_keyplayer(k = 10))And let’s combine and plot the key-players:
cooc_books_1_graph %>%
bind_graphs(cooc_books_2_graph) %>%
bind_graphs(cooc_books_3_graph) %>%
bind_graphs(cooc_books_4_graph) %>%
bind_graphs(cooc_books_5_graph) %>%
ggraph(layout = "fr") +
facet_nodes( ~ book, scales = "free", ncol = 1) +
geom_edge_density(aes(fill = weight)) +
geom_edge_link(aes(edge_width = weight), alpha = 0.2) +
geom_node_point(aes(color = factor(keyplayer)), size = 3) +
geom_node_text(aes(label = name), color = "black", size = 3, repel = TRUE) +
theme_graph() +
scale_colour_manual(values = c(cols[2], cols[1]))
The networks and key-players of the five different books also offer a few surprises but also a lot that reflects the narrative quite well. I’m not going to go into details here as that would go a bit too far for an R-related blog - but if you are interested in in-depth discussions about the books, email me… ;-)
More info
You can find more info about
tidygraphhereggraphhereinfluenceRhere- and DataCamp has a Python project for the same data set here
sessionInfo()## R version 3.4.3 (2017-11-30)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS High Sierra 10.13.4
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.4/Resources/lib/libRlapack.dylib
##
## locale:
## [1] de_DE.UTF-8/de_DE.UTF-8/de_DE.UTF-8/C/de_DE.UTF-8/de_DE.UTF-8
##
## attached base packages:
## [1] methods stats graphics grDevices utils datasets base
##
## other attached packages:
## [1] bindrcpp_0.2 ggraph_1.0.1 tidygraph_1.1.0
## [4] forcats_0.3.0 stringr_1.3.0 dplyr_0.7.4
## [7] purrr_0.2.4 tidyr_0.8.0 tibble_1.4.2
## [10] ggplot2_2.2.1.9000 tidyverse_1.2.1 readr_1.1.1
##
## loaded via a namespace (and not attached):
## [1] nlme_3.1-131.1 bitops_1.0-6 lubridate_1.7.3
## [4] RColorBrewer_1.1-2 httr_1.3.1 prabclus_2.2-6
## [7] rprojroot_1.3-2 tools_3.4.3 backports_1.1.2
## [10] utf8_1.1.3 R6_2.2.2 KernSmooth_2.23-15
## [13] lazyeval_0.2.1 colorspace_1.3-2 trimcluster_0.1-2
## [16] nnet_7.3-12 withr_2.1.1.9000 tidyselect_0.2.4
## [19] gridExtra_2.3 mnormt_1.5-5 compiler_3.4.3
## [22] cli_1.0.0 rvest_0.3.2 TSP_1.1-5
## [25] influenceR_0.1.0 xml2_1.2.0 labeling_0.3
## [28] bookdown_0.7 diptest_0.75-7 caTools_1.17.1
## [31] scales_0.5.0.9000 DEoptimR_1.0-8 robustbase_0.92-8
## [34] mvtnorm_1.0-7 psych_1.7.8 digest_0.6.15
## [37] foreign_0.8-69 rmarkdown_1.8 pkgconfig_2.0.1
## [40] htmltools_0.3.6 rlang_0.2.0.9000 readxl_1.0.0
## [43] rstudioapi_0.7 bindr_0.1 jsonlite_1.5
## [46] mclust_5.4 gtools_3.5.0 dendextend_1.7.0
## [49] magrittr_1.5 modeltools_0.2-21 Rcpp_0.12.15
## [52] munsell_0.4.3 viridis_0.5.0 stringi_1.1.6
## [55] whisker_0.3-2 yaml_2.1.17 MASS_7.3-49
## [58] flexmix_2.3-14 gplots_3.0.1 plyr_1.8.4
## [61] grid_3.4.3 parallel_3.4.3 gdata_2.18.0
## [64] ggrepel_0.7.0 crayon_1.3.4 udunits2_0.13
## [67] lattice_0.20-35 haven_1.1.1 hms_0.4.1
## [70] knitr_1.20 pillar_1.2.1 igraph_1.1.2
## [73] fpc_2.1-11 stats4_3.4.3 reshape2_1.4.3
## [76] codetools_0.2-15 glue_1.2.0 gclus_1.3.1
## [79] evaluate_0.10.1 blogdown_0.5 modelr_0.1.1
## [82] tweenr_0.1.5 foreach_1.4.4 cellranger_1.1.0
## [85] gtable_0.2.0 kernlab_0.9-25 assertthat_0.2.0
## [88] xfun_0.1 ggforce_0.1.1 broom_0.4.3
## [91] class_7.3-14 viridisLite_0.3.0 seriation_1.2-3
## [94] iterators_1.0.9 registry_0.5 units_0.5-1
## [97] cluster_2.0.6